http://acmicpc.net/problem/1011

{코드}
from math import sqrt
for _ in range(int(input())):
x, y = map(int, input().split())
dif = y-x
if dif <= 3:
print(dif)
else:
t = int(sqrt(y-x))
if dif == t**2:
print(2*t-1)
elif t**2 < dif <= t**2 + t:
print(2*t)
elif t**2 + t < dif <= t**2 + 2*t:
print(2*t+1){설명}
이 문제는 규칙을 파악하는 것이 매우 중요한 문제입니다.
해당 문제의 답은 다음과 같이 전개됩니다.
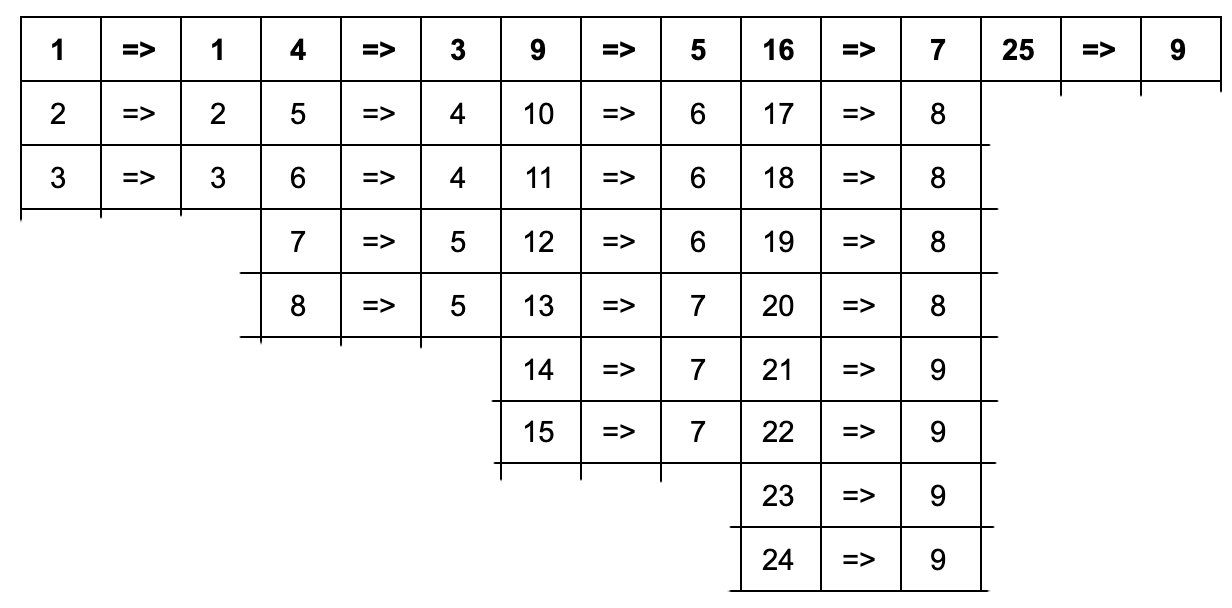
먼저, 수가 3보다 같거나 작은 경우 답은 해당 수와 같습니다.
아닌 경우, 각 수보다 작거나 같은 제곱수의 양의 제곱근(예: 25인 경우 5, 20인 경우 4)을 t로 가정하겠습니다.
이때 만약 수가 제곱수라면, 즉 t의 제곱과 같다면 답은 2*t-1이 됩니다.
또한, 어떤 제곱수에 t를 한번 더한 범위 안의 수들의 답은 2*t이며
해당 범위에 t를 한번 더 더하면 그 수들의 답은 2*t+1입니다.
어떤 수 n과 n+1 각각의 제곱 사이의 수의 개수는 2n과 같으므로 위보다 더 큰 범위의 수는 다음 제곱수와 연관됩니다.
( (n+1)^2와 n^2 사이의 수 = n^2+2n+1 - n^2 - 1 = 2n)
여기서부터는 더욱 자세한 설명이 이어집니다.
일단 우주선의 이동 거리를 각 단계별로 표시하면 1, 2,...t...2, 1과 같이 증가하다가 다시 감소하는 형태를 띠게 됩니다.
(t는 위의 t와 동일 개념)
그리고 제곱수의 경우 무조건 1, 2....t...2...1과 같이 1부터 제곱근까지 1씩 증가하다가 다시 1까지 1씩 감소합니다.
(16의 경우 - 1, 2, 3, 4, 3, 2, 1)이며 이 값을 계산하면 다음과 같습니다.

그러면 제곱수 < n < 제곱수 + 제곱근을 더한 범위의 수들은 1~t를 제곱수를 단계별로 표시한 것에 하나만 추가하면 되고
제곱수+제곱근 < n <=제곱수+2 제곱근의 범위의 수들은 제곱수에 제곱근과 1~t를 단계별로 표시한 것에 하나씩만 추가하면 된다.
예로 20과 21을 표시하면 20은 16+4이므로 1+2+3+4+4+3+2+1이며 21은 16+4+1이므로 1+2+3+4+4+3+2+1+1이다.
'알고리즘 공부 > BOJ백준 풀이' 카테고리의 다른 글
| [백준 2581번-파이썬/Python] 소수 (0) | 2020.12.17 |
|---|---|
| [백준 1978번-파이썬/Python] 소수 찾기 (0) | 2020.12.17 |
| [백준 2775번-파이썬/Python] 부녀회장이 될거야 (0) | 2020.11.15 |
| [백준 10250번-파이썬/Python] ACM 호텔 (0) | 2020.10.31 |
| [백준 2869번-파이썬/Python] 달팽이는 올라가고 싶다 (0) | 2020.10.31 |
![[백준 1011번-파이썬/Python] Fly me to Alpha Centauri](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FRYx9r%2FbtqQn0C5vP4%2FAAAAAAAAAAAAAAAAAAAAAMxcZNkll9rnNNQBLeFi_RMdn8NytHm3TbFKxXr9pKH4%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1767193199%26allow_ip%3D%26allow_referer%3D%26signature%3D316fEmiXnsJgnjoaKg4JPDpL41g%253D)